Previous Posts

Simulated Knitting (post)

I created a KnittedGraph class (subclassing of Python's igraph graph class) with methods corresponding to common operations performed while knitting:

g = KnittedGraph()
g.AddStitches(n)
g.ConnectToZero() # join with the first stitch for a circular shape 
g.NewRow() # start a new row of stitches
g.Increase() # two stitches in new row connect to one stitch in old
#(etc.)

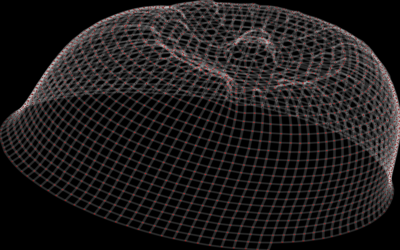
I then embed the graphs in 3D space. Here's a hat I made this way:

2D Embeddings from Unsupervised Random Forests (1, 2)

There are all sorts of ways to embed high-dimensional data in low dimensions for visualization. Here's one:

1. Given some set of high dimensional examples, build a random forest to distinguish examples from non-examples.
2. Assign similarities to pairs of examples based on how often they are in leaf nodes together.
3. Map examples to 2D in such a way that similarity decreases decreases with Euclidean 2D distance (I used multidimensional scaling for this).

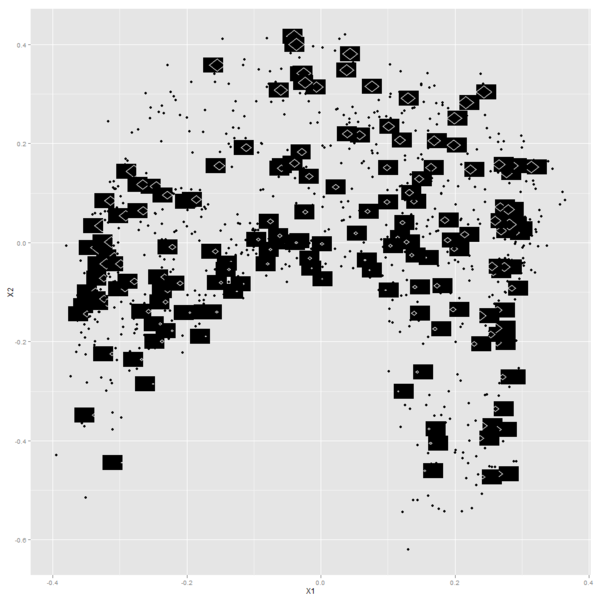
Here's the result of doing this on a set of diamond shapes I constructed. I like how it turned out:

A Bayesian Model for a Function Increasing by Chi-Squared Jumps (in Stan) (post)

In this paper, Andrew Gelman mentions a neat example where there's a big problem with a naive approach to putting a Bayesian prior on functions that are constrained to be increasing. So I thought about what sort of prior would make sense for such functions, and fit the models in Stan.

I enjoyed Andrew's description of my attempt: "... it has a charming DIY flavor that might make you feel that you too can patch together a model in Stan to do what you need."

Lissijous Curves JSFiddle

Some JavaScript I wrote (using d3) to mimick what an oscilloscope I saw at the Exploratorium was doing:

Visualization of the Weirstrass Elliptic Function as a Sum of Terms

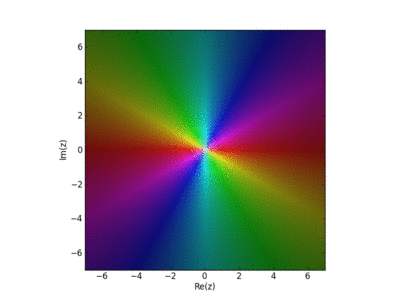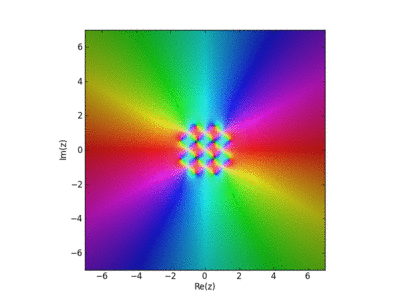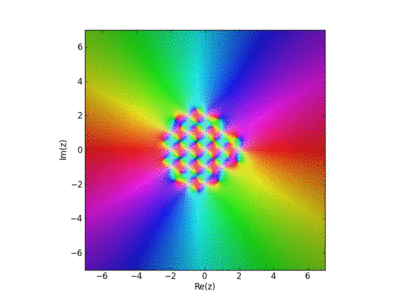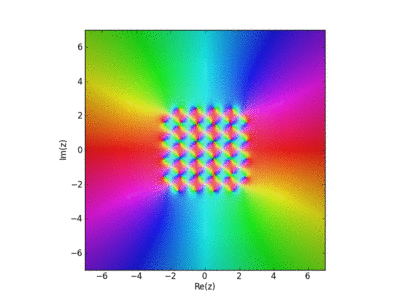
John Baez used this in his AMS blog Visual Insight.